Let’s Build a 4-bit Computer! -Instruction Set Adenium

Oops, I made a big mistake! Let’s fix it.

In my last post on the 4-bit computer, I wanted to end it with creating an adder, but I realized that I may need to give more theory and detail than expected, which unfortunately means I would have needed to write an extremely long post. So today, we have part two.

If you want something less in-depth, I have a short summary on how difficult it is to run AI Image Generation well.

Let’s talk about shifts.

This week, I want to focus in on the last of the core operations.

10 is lshift, shift the contents of the register left, with wraparound.

11 is rshift, shift the contents of the register right, with wraparound.

12 is ror, an or on the rightmost bits.

13 is rand, an and on the rightmost bits.

14 is rnot, a not on the last bit.

So what are lshift and rshift?

Assume a new command: print with the syntax print value. We will ignore implementation for now.

What is the outcome of this code?

uload 0001 - a
print a
lshift a
print a

uload takes a binary string, and puts it into a register that can be named, that is, we save a variable. In a more familiar format all uload does is:

a=1

So the output of our code should be:

0001

0010

Ok, cool. Did we pad with that zero? Where did the zero on the left go? Remember that the two shifts have wraparound. The zero on the right in the second print was on the left in the first print. We effectively took it from the left and pushed it to the right.

This now allows us to do every operation needed for a fully functional computer. Let’s demonstrate that by building a new instruction: add.

add will have the syntax add in1 in2 -> out

I’m also going to make an assumption that there’s a register built in called zeroes, that is just a register of zeros.

For reference, we are building this: and chaining it together.

By Inductiveload — Own work, Public Domain, https://commons.wikimedia.org/w/index.php?curid=1023334

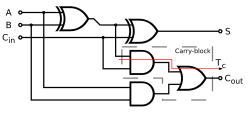
#Helper xor on the right bit. (also a great gate to have on hand)
compute rxor a b - out{

  #Remember, xor is the same as (a and not b), or (b and not a)

  rand a b - tmp
  rand a b - out
  ror out tmp - tmp
  ok
}

#We need to start by having a full adder implemented
compute radder a, b, c - out cout{
  rxor a b - out
  
  rand c out - cout
  rand a b - tmp
  
  ror cout tmp - cout

  rxor out c - out

  ok
}

We have two options on how to implement this, create a loop function, or just do repeats. I have everything I need to make a loop, but it’s going to be constructed with loadp and an assumption. Unfortunately that’s going to look a lot like a goto and I need to put some more thought into how I want it to work and hope there’s some way around that. So to ignore that problem for a little bit, I’m just going to do some loop unrolling. According to Gemini:

Loop unrolling is a compiler optimization technique where the body of a loop is duplicated multiple times within the loop, reducing the number of times the loop condition and increment/decrement instructions are executed.

I’m just going to unroll this to the point there is no loop. Yay for brute force!

Please take note of loop unrolling, it’s an important thing in quantum computing. It’s not my focus here, but I want to note this and focus later.

compute add a b - out cout{
  uload 0000 - c

  radder a b c - out c
  rshift a
  rshift b
  rshift out
  #We want c to be one behind the rest to carry from the last operation
  
  radder a b c - out c
  rshift a
  rshift b
  rshift out
  rshift c

  radder a b c - out c
  rshift a
  rshift b
  rshift out
  rshift c

  radder a b c - out c
  rshift a
  rshift b
  rshift out
  rshift c

  ok
}

Awesome! We got that done, I’m going to throw everything I have here on Github to help with reference, and this is a series I’d love to continue. As far as this series goes, there’s going to be a shift. I’m pausing on this portion and shifting to reversable computing. I hope this portion of the course is helpful to understanding how simple instructions can be used to expand to a full, powerful programming language. We will use this skill to explore quantum computing later.